Due rette dello spazio di definiscono incidenti quando hanno uno ed un solo punto in comune.
Questa è la definizione corretta da dare quando vi trovate di fronte al quesito “quando due rette sono incidenti?”.
Approfondiamo ora l’argomento per avere una spiegazione più completa della casistica.
INDICE:
Quando due rette sono incidenti?
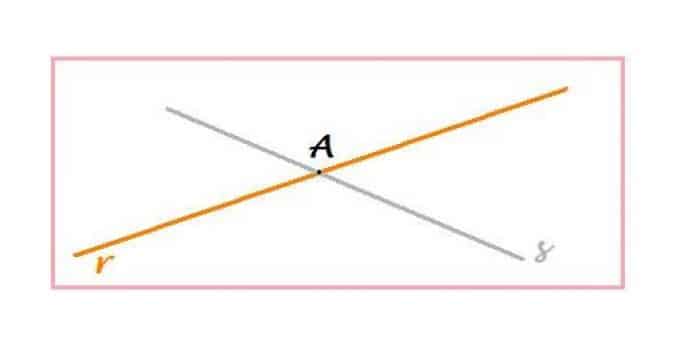
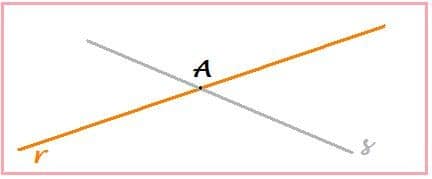
Prendiamo due rette, che indichiamo rispettivamente con le lettere “r” e “s”, come nell’immagine che segue.
Supponiamo che le due rette abbiano in comune un solo punto, che chiamiamo “A”.Le due rette quindi si incontrano nel punto A.
A viene detto punto di intersezione delle due rette “r” ed “s”.
Le rette “r” ed “s” sono incidenti o secanti.
Caratteristiche delle rette incidenti
Le rette devono sempre essere considerate con proiezione all’infinito della loro lunghezza.
Quindi, come detto, si definiscono indicenti quando si intersecano in un solo punto.
r ∩ s = A
Requisito fondamentale affinchè due rette possano essere definitte incidenti, è che esse siano anche complanari, ovvero disposte sullo stesso piano.
Se, al contrario fossero su piani diversi, le rette non avrebbero alcun punto di intersezione pur avendo direzioni che – se sovrapposte e “schiacciacciate” nello stesso piano – mostrerebbero un punto in comune.
Due rette non complanari si dicono “rette sghembe”, e non possono essere incidenti.
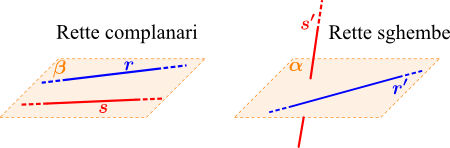
Due rette incidenti devono essere anche complanari
Per dimostrare questa affermazione ci viene in soccorso un teorema della geometria Euclidea, il quale dice che due rette sono complanari se e solo se sono parallele o incidenti.
Quindi per contrapposizione, due rette che non sono ne parallele ne incidenti non appartengono allo stesso piano, e quindi sono rette sghembe.
Rette coincidenti
Se le due rette “r” ed “s” si intersecano in ogni punto, per tutta la loro (infinita) lunghezza, allora si parla di rette coincidenti.
Da tenere presente che due rette complanari o si incontrano in un solo punto (incidenti), o non si incontrano mai (parallele), oppure si incontrano in tutti i loro punti (coincidenti).
Approfondimenti sulle rette
Se vuoi completare la panoramica sulle rette, puoi approfondire il concetto di rette parallele e rette sghembe leggendo i rispettivi articoli.